Procedural Knowledge in Pretraining Drives LLM Reasoning
Authors. Laura Ruis, Maximilian Mozes, Juhan Bae, Siddhartha Rao Kamalakara, Dwarak Talupuru, Acyr Locatelli, Robert Kirk, Tim Rocktäschel, Edward Grefenstette, Max Bartolo
TL;DR. LLMs strategy for mathematical reasoning looks unlike retrieval from the parametric knowledge formed during pretraining. Instead, the models learn to apply procedural knowledge extracted from documents involving similar reasoning processes, either in the form of general descriptions of procedures, or applications of similar procedures. This indicates that we may not need to cover every possible case in the pretraining data: focusing on high-quality data demonstrating procedures across diverse reasoning tasks could be more effective.
Paper. ArXiv
Demo. Coming soon: some of the top and bottom documents per query
Supplement. Supplement
In this post
Background: EK-FAC influence functions
Introduction
Since LLMs entered the stage, there has been a hypothesis prevalent in the community:
Some examples of this hypothesis in the community:
LLM reasoning is prompt-dependent and can be brittle, and they sometimes make funny mistakes that humans would never make. However, most studies concluding that this means LLMs might be doing approximate retrieval when reasoning do not look at the pretraining data. Many studies that do look at pretraining data have shown contamination of evaluation data improves LLM’s performance on benchmarks. However, does that mean the model is always relying on previously seen answers when producing reasoning traces? I set out this project believing they might be, and thought we would uncover data contamination: models relying on the answers to the steps for simple mathematical reasoning questions, or some other form of retrieval that is less interpretable. To test all this, we asked the following research question:
We took a sample of 5 million of two model’s pretraining sequences and ranked them according to how strongly they influence both the likelihood of the model’s reasoning traces for simple mathematical tasks, and the likelihood of the model’s answers to factual questions that require retrieval from parametric knowledge.
To my surprise, we find the opposite of what I thought:
The procedural knowledge models learn from comes in the form of general descriptions of procedures or applications of similar procedures. This finding can inform future pretraining data selection efforts:
Importantly, we do not find evidence for models generalising from pretraining data about one particular type of reasoning to another similar one (e.g. from solving linear equations to calculating slopes of a line between two points). LLM reasoning doesn’t go as far as human’s yet, and it is definitely less robust than that of a focused and trained mathematician, but I’m personally excited to think about how far procedural generalisation from next-token prediction can go.
In this post, I will explain all the pieces of evidence that came together for these findings. For an academic treatise of the findings, refer to the paper. This post will be a complementary source where I can more freely show results from the large amount of data we gathered. We looked at 200 model completions and calculate the influence of 5 million pretraining sequences (covering 2.5B tokens) for each. This required a billion gradient dot-products (and gradients of LLMs are pretty big), as well as estimating over 300B parameters representing second order information of the training objective for a 7B and 35B LLM.
Let’s delve dive in.
The problem
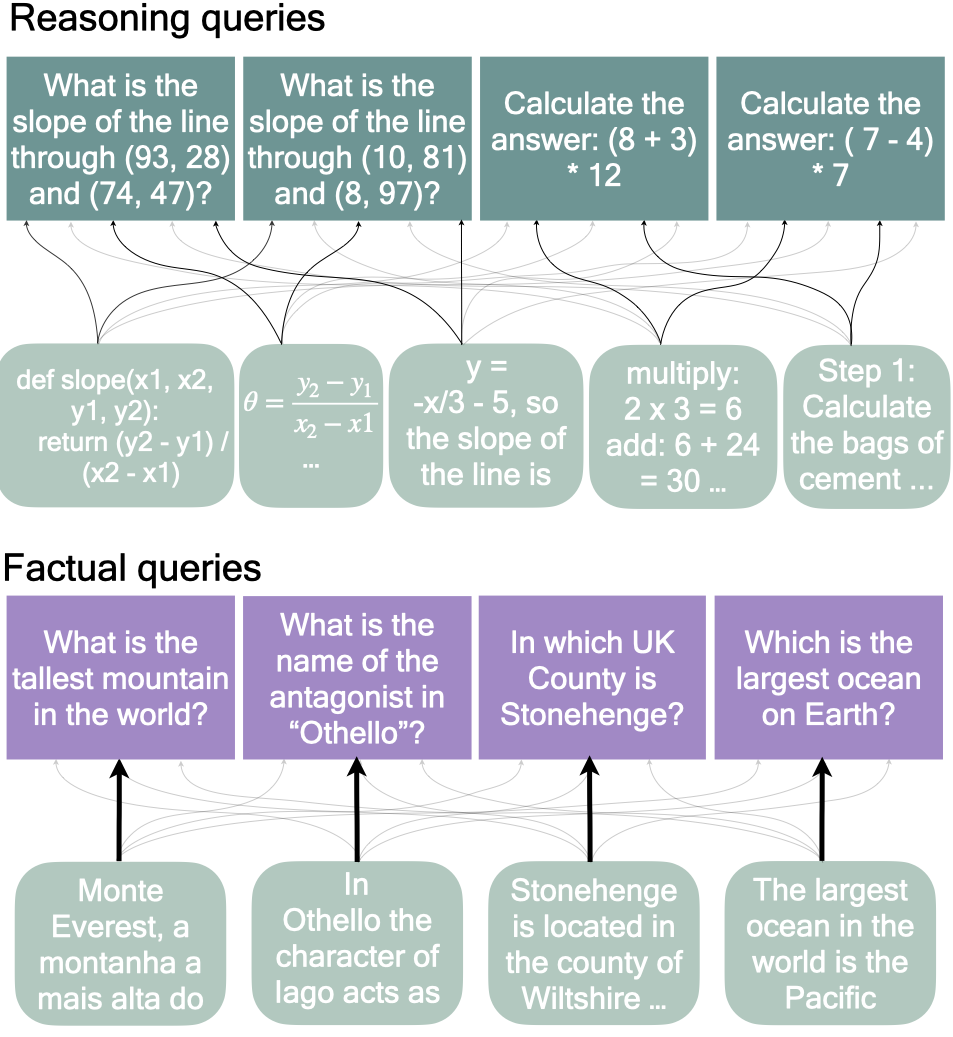
Consider two types of questions. On the left-hand side, we have a factual query that requires retrieving parametric knowledge to answer – at least for a vanilla LLM that does not use any tools. The model needs to retrieve which mountain is the tallest and how high that mountain is. On the right-hand side, a reasoning query is shown that requires answering 7 - 4, and then 3 * 7, to get to the final answer.
How is the model doing that? Is it using a strategy that is similar to what it does on the left-hand side? This would mean it is not very generalisable, because it needs to remember all the answers to reasoning questions and patch them together. This is not an ideal strategy for a task with so much structure as arithmetic. At the same time, it’s not unthinkable the model is doing that for such simple forms of arithmetic. Alternatively, it might be using a more generalisable strategy that can be applied to many different questions of the same type of reasoning, but with different numbers.
Traditionally, we would make sure that it is not possible to use the former strategy and memorise the answer to reasoning questions by properly splitting training data from test data, but this is not possible anymore in the LLM paradigm. In this work, we instead look at the pretraining data that “caused” completions for factual and reasoning questions.
We estimate how including documents in the training set influences completions for the factual queries to get a picture of what it looks like for a model to be doing retrieval from parametric knowledge. We also estimate the influence each document has on the generated reasoning traces, and ask the following questions: what kind of data is influential for the generated reasoning traces? Do we find the answer to the question or the reasoning traces in the most influential data? If not, how otherwise are the documents related to the query? What does the distribution of influence over pretraining documents for reasoning look like compared to the factual retrieval one? Does the model rely heavily on specific documents for the completions, or is the distribution of influence more spread out, with each document contributing less overall? The former fits a retrieval strategy and the latter does not. Do single documents contribute similarly to different questions, which would indicate they contain generalisable knowledge, or is the set of influential documents for different questions very different, which would fit more with a retrieval strategy? We look into all these questions to determine whether the model is doing retrieval for reasoning or another more generalisable strategy.
Background: EK-FAC influence functions
Before we discuss the experimental setup to answers the above questions, I will briefly explain the method we are using. I said earlier we “estimate how including documents in the training set influences completions” and we “look at the pretraining data that ‘cause’ completions”. To do this, we use EK-FAC influence functions. For details, refer to the paper, or to the much more comprehensive background and methods section (2 and 3) in Grosse et al’s paper. I will mention here that EK-FAC influence functions estimate the following counterfactual question:
These kinds of influence functions have a similar computational complexity as pretraining itself (it requires two forward-backward passes for every pair of training datapoints and model completions you look at, as well as estimating second order information for each model), which is why we look at a sample of the pretraining data (2.5B tokens). In our work, we rely heavily on Grosse et al’s efforts to make EK-FAC influence functions work for large-scale Transformers, and we borrow their terminology throughout the paper, calling the prompt-completion pairs (factual and reasoning questions) we look at ‘queries’ and the pretraining data ‘documents’. Further, in Appendix A.1 of the paper we do several counterfactual re-training experiments to show that EK-FAC influence functions also estimate the effect of documents on the accuracy of text generated by next-token prediction.
Experimental setup
We use the following pipeline of generating rankings over pretraining data for factual and reasoning questions.
We take a set of 5 million documents spanning 2.5B tokens that are equally distributed as the pretraining distribution, and use influence functions to estimate their effect on the likelihood of 40 factual and 40 reasoning questions for two models of different sizes (Cohere’s Command R 7B and 35B, trained on the same data). We do the same for a set of 20 control questions for each model that are superficially similar to the reasoning and factual questions, but do not require factual retrieval or reasoning. I’ll discuss those control questions in more detail when it becomes relevant. All in all, we create 200 rankings over 5 million documents each, from most positively influential to most negatively influential.
We look at three mathematical tasks that the 7B and 35B can do reasonably well with zero-shot chain-of-thought. Namely, two-step arithmetic for the 7B, calculating the slopes between two points for both the 7B and 35B (so we can compare results between models for the same prompts), and solving linear equations for the 35B. To find tasks the model can do reasonably well zero-shot (with an accuracy of 80% for a larger set of 100 questions), we had to restrict coefficients and variables. For example, for two-step arithmetic, the numbers we use are between 0 and 20, and the answer is always positive. For calculating slopes, the coefficients are between 0 and 100 (answers can be negative). For solving linear equations, the coefficients are between 0 and 100, the answer is always positive, and we restrict the variable to be x. We additionally make sure the questions never require outputting a fraction.
An example of two-step arithmetic, completion by the 7B model:
An example of calculating the slopes between two points, with completions by the 7B and 35B (note that both completions are off by sign, but the steps the model takes are reasonable):
And finally, an example of solving for x in linear equations, with a completion by the 35B model.
We compare to completions for factual questions. Let’s have a look at one example that is part of the factual set for both the 7B and the 35B:
16 of 40 questions in the factual set for the 7B and 35B overlap, and 23 are different. This is because we wanted 20 questions the model gets wrong, and 20 it gets right, to investigate failures of factual retrieval. The example above in the problem section, about the Mount Everest, is only part of the 7B set. All in all, we have 20 arithmetic questions for the 7B, 20 slopes questions for both, 20 linear questions for the 35B and 40 factual questions each. As mentioned, we also have 20 control questions per model, which we discuss when they become relevant. All queries can be found in the demo and the supplement.
Findings
To answer the above questions about LLM generalisation for reasoning, we do both quantitative and qualitative analyses. For each finding discussed below, we add a dropdown with a deep-dive into the results that give additional insights. These are usually taken from the appendix in the main paper, and can be skipped unless you want more insight into the findings. They do provide a much deeper understanding of the results in this paper. For example, for the correlations found in finding 1, we investigate what drives them in the deep-dive. Further, for the qualitative findings we add a lot of examples from the pretraining data in the deep-dive dropdowns. This makes them quite long, but at the same time, it’s a lot of fun to look at pretraining data.
Quantitative findings
In the quantitative section of the findings, we will look into the following questions:
- Do single documents contribute similarly to different questions, which would indicate they contain generalisable knowledge, or is the set of influential documents for different questions very different, which would fit more with a retrieval strategy? (Finding 1)
- Does the model rely heavily on specific documents for the completions, or is the distribution of influence more spread out, with each document contributing less overall? The former fits a retrieval strategy and the latter does not. (Finding 2)
At the end of each quantitative finding section (outside of the deep-dive dropdowns), we briefly discuss the differences between the 7B and 35B model in a small section titled 7B vs 35B (here for finding 1 and here for finding 2). This is again usually appendix stuff, as the difference between the 7B and 35B is not central to the thesis in this paper, but they give interesting insights into the learning dynamics of LLMs. For example, at the end of finding 1 we uncover that there is almost no correlation between what the 7B learns from data with what the 35B learns from the same data.
Before we can interpret these results, we need to briefly discuss the score influence functions compute.
If a document has an influence score of \(1\) for a particular query, it means influence functions estimate that including it in the pretraining set increases the log-likelihood of the completion by \(1\). Now, you might have noticed that all our completions have a different number of tokens. To make them comparable, we divide all influence scores by the information content in the query completion under the model (i.e. the query nats, which is essentially just the query log-likelihood).
Now we can discuss quantitative findings.
How generalisable is the information the influence scores pick up on?
The first thing we look at is how often documents are similarly influential for multiple different queries. If models are relying on documents that contain ‘general’ knowledge that is applicable to any query with the same task (e.g. queries that require finding the slope between two points for many different points), we would expect there to be a significant correlation in the influence scores for these queries.
We calculate the Pearson’s R correlation of all 5 million document influences for pairs of queries, and find that scores often correlate when both queries concern the same mathematical task. This is depicted in the figures below, left for the 7B model and right for the 35B. Shown is a heatmap of all query combinations. On both axes are the queries from 1 to 100, of which the first 40 are factual, the next 20 are two-step arithmetic queries for the 7B and 20 linear equation questions for the 35B, then 20 slopes questions, and finally 20 control questions. What we can see is that, bar some exceptions which we will discuss in more detail in the deep-dive below, there are mainly strong correlations between queries of the same reasoning type.
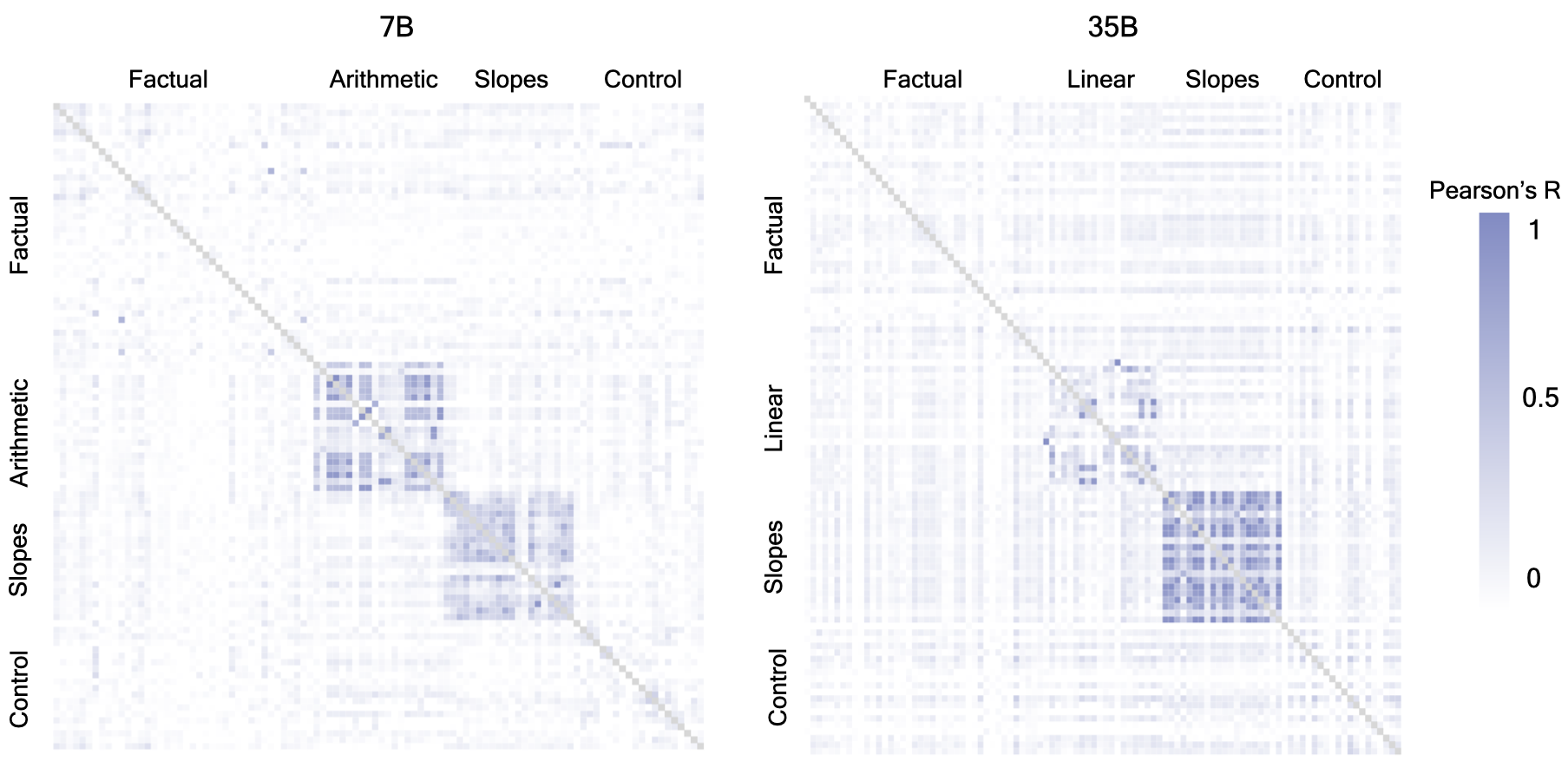
By contrast, there is usually no correlation between factual queries, or other combinations (e.g. a factual query and a reasoning query). This means that the same document often has a similar influence on completions that require applying the same procedure to different numbers. We show this schematically below; arrows of similar influence can go from documents to multiple reasoning questions of the same type, but generally this does not happen for factual questions, or across different reasoning types.
These correlations indicate that influence scores for reasoning traces pick up on procedural knowledge in the pretraining data. In the drop-down below, we investigate what drives the correlations. We share all correlations between queries in the supplement.
Deep-dive into finding 1 (click to view)
In this deep-dive dropdown, we take a closer look at what might cause these correlations. This is material from the Appendix of the main paper, so feel free to collapse and skip to go to Finding 2 below. What we will uncover in this section is that correlations seem driven by a combination of formatting and underlying procedure. Further, we highlight some of the control queries, how they are similar to the main queries superficially but do not require reasoning or factual retrieval, and what the correlations with control queries can inform us of.
Now take a look at an example of a combination of a reasoning and a reasoning control query. On the left a regular slopes reasoning query is shown, and on the right-hand side a reasoning control query that is designed to be similar but that does not require any reasoning. By contrast, the correlation between the two queries below is 0.2.
To show that formatting also strongly influences correlations, we highlight the below example of query-combination that results in a correlation of 0.55. We note that the underlying mathematical task is the same, and even requires one identical step in terms of numbers, but the formatting is different, and the correlation is lower.
We also sometimes observe higher correlations for control queries, and these seem driven by formatting. For example, below two query examples for which the Pearson's R of their document influences is 0.38, both from the reasoning control set for the 7B model. We observe that the formatting is very similar, but the correlation is still lower than for the reasoning queries above.
The highest correlation between two queries we observe is between the following arithmetic queries. We see that the formatting is identical, but again applied to different numbers. For these queries, the reasoning steps do share similarities in terms of numbers. The first step both requires subtracting 4, and the next step requires multiplying by 7. However, the answer to both reasoning steps is different for the two queries. The Pearson's R is 0.96.
The highest correlation we find between two factual queries for the 7B is 0.64. This is an outlier, an the average correlation for queries of the type factual is 0.06 for the 7B and 0.03 for the 35B. We see below that these queries both are similar forms of factual questions, namely what-questions. Further, the completion is formatted very similarly, repeating the question and including quotation marks around the answer.
For the mathematical task of finding x for a linear equation, we do not find a lot of high correlations. There are a few, but the average correlation is 0.16. In the main paper, we discuss that this might be because the model cannot very robustly solve linear equations for x. In order to get a performance of at least 80% of the 35B model on this task, we had to restrict all calculations to lead to a positive x, and it only worked for x, not any other variable such as y or z. We share all correlations between queries in the supplemental material of the paper. The results in this section substantiate the main finding in this work: influence scores for reasoning traces seem to pick up on information that is applicable regardless of which specific numbers are used.
7B vs 35B
An additional finding that is not central to the research question in this work, but is nonetheless interesting, is that there is almost no correlation between the influence scores of the two different models. We have 36 queries that share the same prompt for the 7B and 35B (16 factual questions, and 20 slopes reasoning questions) and we can calculate the Pearson’s R of the queries with matched prompts (i.e. 36 combinations). The average correlation of influence scores is 0.02 Pearson’s R (if we only look at the slopes questions the average correlation is 0.03). The maximum correlation we find is 0.19, for the question “What is the capital of Belgium?”, which we know from the deep-dive above is not a comparatively high score correlation. Interestingly, for this query, both models produced the exact same completion, and still the correlation is comparatively low. All other query combinations correlate with a Pearson’s R below 0.11. This connects to a finding from Grosse et al. (larger models rely on data that is more abstractly related to the prompt): the 35B model relies on very different pretraining data than the 7B, and the same pretraining documents influence completions for the same prompt very differently.
How strongly do models rely on specific documents?
If models are using a retrieval strategy, we would expect them to strongly rely on ‘specific’ documents (i.e. those containing the information to be retrieved). This is what we find for the factual questions, but not for the reasoning questions. Below, we see the total influence for different portions of the positive parts of the rankings (top-\(k\) percentiles). For example, the value at the y-axis for the top-20 percentile is the average sum of total influence of the top 20% of the ranking for all queries in that group. The same plots for the negative portions of the rankings look similar, and the discussion below applies equally to all parts of the rankings. The negative plots can be found in appendix A.9.2. of the paper.
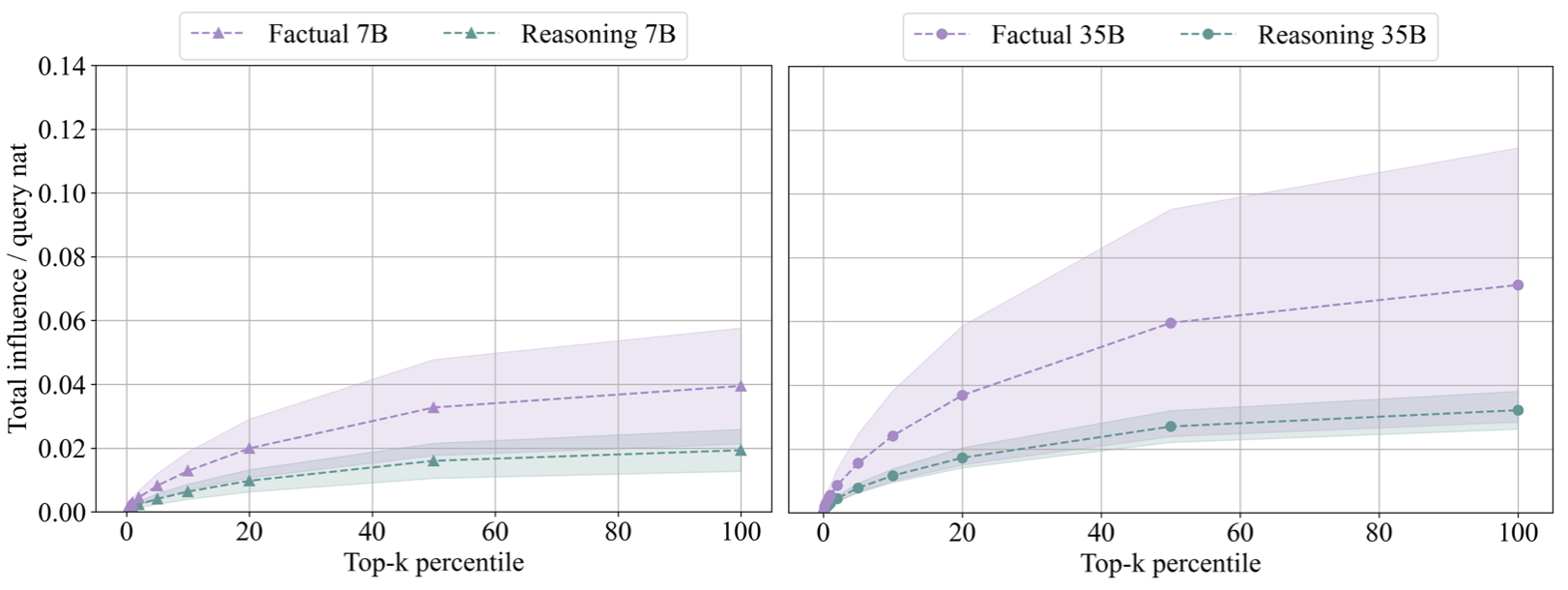
If we compare the results between reasoning queries and factual queries for the same model, the first thing to note is that on average the total magnitude of influence contained in any part of the rankings is much smaller for reasoning queries than for factual queries. The second thing to note is that the total magnitude of influence is much more volatile for factual questions than for reasoning questions. The first result means that, on average, the models rely on individual documents within our set less for generating reasoning traces than for answering factual questions. The second result indicates that for the factual questions the model relies on more ‘specific’ and infrequent documents: for a factual question it is more up to chance whether relatively highly influential documents (w.r.t. influence of documents for other factual questions) are part of the pretraining sample or not.
For the above plots, we sum different numbers of documents for each query for the same x-axis point (each query has a different number of total positive documents). We show in the Appendix A.9.2 of the main paper that the results are the same if we show the absolute number of documents on the x-axis instead.
In the drop-down below, we look into the distribution of influence over the rankings. This is a relative metric w.r.t. the total influence for a query, as opposed to the absolute magnitude we analysed just now.
Deep-dive into finding 2 (click to view)
Note that this is a relative comparison, and the total absolute magnitude is still much higher for factual questions on average than for reasoning questions. Again, the bottom parts of the ranking look similar (shown in the Appendix A.9.3. of the main paper). Additionally, if we only look at the queries the models get right (meaning we also filter out queries with failures of retrieval), the 7B also shows a slightly steeper increase in total relative influence score, shown below.
The error bars overlap here, but in the main paper we shot that the difference is significant if we look at the top 0.02% of the rankings. We do this by fitting a power law to the top 500 documents of the ranking, and comparing the slopes. The results can be seen in the Table below:
Note: "*" indicates a p-value below 0.1, and "**" indicates a p-value below 0.05, based on an independent T-test between the slopes of the factual vs. reasoning queries.
The distribution of influence over documents tells us something about the type of generalisation strategy the model is likely using; the more documents that contribute to each nat of query information (i.e. the more spread out the total influence), the more documents the model is relying on to produce the completion. One would perhaps expect a steeper power law for factual questions than for reasoning (meaning more of the total positive influence contained at the top parts of the ranking), but our results show evidence for the opposite. Perhaps a model needs to generalise from a broader set of documents for factual retrieval than for reasoning because it needs to see the same information more often to memorise it. This is supported by the finding that for factual questions the model gets right the answer often shows up multiple times in the top 0.01% most influential data (discussed below in the qualitative sections on finding the answer to questions). However, we note in the main paper and in Appendix A.9.3 that there is a chance this finding is explained by noise, where we note that for the reasoning query with the steepest power law, the top 1 document is qualitatively entirely unrelated to the prompt. Future work must elicidate whether such documents are actually influential or represent noise.
7B vs 35B
In order to comment on the differences between the 7B and the 35B model, we plot the same result for only the overlapping queries. Of all queries only 36 have the same prompt (see the Method section above). For the overlapping queries, the prompts are the same but the completions are by different models.
The first thing to note is that the everything is shifted up for the 35B model. The second thing to note is that the magnitude of influence for factual queries is even more volatile for the 35B than for the 7B. This holds both for reasoning and factual questions, but more strongly for the latter.
This could mean that the 35B model can learn relatively more from highly relevant documents for the same question than the 7B (indicating higher data efficiency). We can test this hypothesis by directly comparing the influence scores for the queries that have overlapping prompts between models. For each overlapping query, we divide the absolute value of the top 50,000 influence scores of documents for the 35B model by the scores for the 7B model. This gives a ‘multiplier’ that indicates how much larger the influence scores for the 35B model are than those for the 7B usually in the top portions of the ranking. For the factual queries, we find that 81% of the influence scores of the top 50,000 document are larger for the 35B than for the 7B. The average multiplier is 1.9 (+/- 0.09). For the reasoning queries, the percentage is 54%, and the average multiplier is 1.3 (+/- 0.11). If we instead look at the top 50,000 most negatively influential documents, the average multiplier for influence scores for factual questions is 0.85, and only 20% of documents have a multiplier larger than 1. By contrast, the negative score multiplier for the reasoning questions is 1.53 and 81% of the bottom 50,000 documents have a larger absolute influence for the 35B than for the 7B.
Taken together, these results shows that the influence scores of the most influential documents for the 35B (positively or negatively) are usually larger for the reasoning questions, but only by a relatively small margin. The highly positively influential scores are usually much higher for the factual questions, especially because this multiplier represents a much larger absolute number. This indicates that the 35B model can learn more from the same set of documents, mainly for factual questions.
Qualitative findings
In the qualitative section of the findings, we will look into the following questions:
- Do we find the answer to the question or the reasoning traces in the most influential data? (Finding 3)
- If not, how otherwise are the documents related to the query? What kind of data is influential for the generated reasoning traces? (Finding 4)
- Which pretraining data sources are overrepresented with respect to the training distribution in the most positively and negatively influential data? (Finding 5)
Again, I will discuss main findings, and then provide a deep-dive section for each. These deep-dives will contain a lot of pretraining datapoints, like those with the answers to factual questions and reasoning questions, and we will additionally refer to the demo where readers can look through some of the top and bottom most influential sequences for each query independently.
Do models rely on the answers to reasoning questions?
We search the top 500 (top 0.01%) of the rankings for each factual and reasoning query for the answers in two ways: a manual search through the top 100 documents with keyword overlap and an automatic search with Command R+ (100B) independent of keyword overlap. For the the factual questions, we search for the full answer in a single document. For the reasoning questions, we search for the answers to each reasoning step. If answers to all reasoning steps occur in separate documents, we also count that as an answer occurrence. For details on how we search the documents, refer to the paper Section 5.2 (Finding 3). The results are shown below.
For the factual queries the model gets correct, we find the answer to 55% in the top documents for the 7B, and 30% for the 35B. For both models, we find the answer to a factual query it gets wrong once. By contrast, we find the answer to a reasoning question twice for the 7B (7% of reasoning queries it gets correct), and never for the 35B (0%). Further, the answer to the factual questions often show up multiple times in the top 500 documents. For the 7B, we find the answer to factual queries 30 times, and 15 times for the 35B.
We investigate the hypothesis that the answers to the reasoning questions are not present in the larger set of 5M documents by doing a search over a subset of these 5M documents filtered through keyword matches. We uncover answers to a reasoning step for 13 of 20 arithmetic reasoning queries that do not show up in the top 500 documents, and a full answer (all reasoning steps) for 1 of 20. For the slopes and linear equation questions, we find answers to 3 reasoning steps that do not show up as highly influential. We expect many more to be present in the larger set that elude the keyword search.
In the deep-dive below, we look at the documents that contain answers for factual and reasoning questions, both when they are relatively influential, and when they are not. Additionally, we give some examples of crosslingual transfer (when the answer to factual questions shows up in languages besides English).
Deep-dive into finding 3 (click to view)
To get some more qualitative insight into how answers show up, in this section we highlight some examples. We share some documents with answers in the supplemental material, and they can be found in the demo as well. For factual questions, it happens quite often that the answer to the question shows up as highly influential in multiple documents in the top 10. For example, for the factual question "What is the tallest mountain in the world and how tall is it?", the answer shows up at ranks 1, 4, 6, and 7. The document at rank 1 (the most positively influential one), is the following (we underlined the answer in the document):
This question is apparently a very common one in the pretraining data. What about a more "niche" question? We ask "What is the common name for the larva of a housefly?", and the answer shows up at rank 6 for the 35B model (the same question is in the query set for the 7B, but the answer does not show up as highly influential there).
Another example of a factual question for which the answer shows up often is "Which artist drew 32 canvases of Campbell’s soup cans?". The answer shows up in 5 of the top 500 documents, at rank 3, 13, 27, 31, and 63. Below, we show the document with the answer at rank 3. The others can be found in the demo or supplement.
By contrast, the answer to only two reasoning questions show up for the 7B, and never for the 35B. For one of those, the answer to reasoning steps is separately found in a document at rank 67 and 83, and for the other at rank 2 and 68. We show the latter documents with the answers to reasoning steps below.
Note that to parse the answer to the reasoning step 5 - 3 = 2 that can be found in the above document, one already needs to understand notation. Further, this particular document is in the top 10 for 11/20 arithmetic queries, so it seems to be influential mainly for other reasons than the answer showing up. By contrast, the above document with the answer to the housefly question never shows up in the top 10 of other queries, and the rank 1 document for the Mount Everest question shows up in the top 10 for 4/40 other factual queries (and it happens to have an answer to another factual query as well, on the largest ocean in the world). The answer to the second reasoning step (2 * 12 = 24), can be found below:
Apart from one, for none of the other arithmetic queries answers to reasoning steps show up as highly influential, though we find answers to reasoning steps for 11 out of the 20 in the larger pretraining sample. For example, one document at rank 2140 has the answer to 5 + 4 = 9:
All in all, the answers to reasoning steps do not seem to drive influence. More often than not, even if we find the answer to reasoning steps in the 5M documents, it is not highly influential. By contrast, the answers to factual questions show up often as highly influential.
7B vs 35B
We should take care not to interpret the difference in amount of times answers show up for the 7B versus the 35B (55% versus 30%). These numbers are not comparable, because only 16/40 factual questions are the same between models. We believe the answers show up less in our subset of 5M pretraining documents for the 35B because the questions are much more “niche”. For example, we ask the 35B “In what year did the Beinecke library open”?
How are the top most influential documents related to the reasoning queries?
If it is not the answers to reasoning questions, what aspects drive influence? For the slope questions, of which we have 20 that are the same for both models, many documents surface as highly influential that show how to calculate the slope between two points in code or math. For the 7B model, documents that present procedural knowledge on how to calculate the slope in either code or math show up in the top 100 documents for 16/20 queries (38 times), and for the 35B model they show up for all queries (51 times). All together, we manually find 7 unique documents that implement the slope in code in the top 100 documents, and 13 that present equations for calculating the slope. The 7B model relies on 18 of these documents for its completions (meaning 18 different ones appear in the top 100 documents for all queries), and the 35B on 8. An example of a highly influential document implementing the solution in JavaScript (left) and in maths (right):
These are redacted versions of real pretraining documents, and in the deep-dive below we share some additional full document examples.
We do a more systematic analysis of how the top 500 documents relate to each query by giving query-document pairs to Command R+ (a more capable 100B model), and asking it to choose one or more keywords from a list of predefined keywords that describe the relationship of the document to the query. For the prompts used, see Appendix A.6. In the deep-dive below, we show the results and give some examples of the most common keywords chosen for each task-model pair. What stands out, is that for arithmetic the most top 500 documents usually concern similar arithmetic operations on other numbers (e.g. much larger or smaller) and code with arithmetic. For the slope questions, by contrast, the most common relation is similar arithmetic on similar numbers, and also code with arithmetic. For the linear equation questions, the most common keywords chosen are math that contains unsolved linear equations, and also similar algebraic operations on similar numbers.
Again, the deep-dive below mainly shows examples of query-document pairs, as well as the results for the analysis using Command R+ to characterise the relationship between the reasoning queries and top 500 documents.
Deep-dive into finding 4 (click to view)
Below, for each model and task pair (7B and 35B, with tasks arithmetic, slopes, and linear equations), we show the counts of the keywords Command R+ assigned to query-document pairs together with an illustrative example of a query-document-keyword pair. Note that most keywords can occur at most 10000 (= 500 documents x 20 reasoning task queries) times, but some can occur more often. This happens when we group multiple keywords together. We mention below whenever this is the case. Additionally, if the chosen keyword was "other types of maths", the prompt asked the model to give a description of the other type of math if that keyword was chosen, and it quite often chooses "other types of maths" multiple times for the same query-document pair with different specifications.
The most common keywords, besides other, are similar arithmetic on other numbers and code that contains arithmetic. These keywords are given to almost half of the query-document pairs. Below, we show an example of a query-document pair that was given both the keyword similar arithmetic on similar numbers, and similar arithmetic on other numbers, among others.
The model gave the following justification for choosing these keywords:
As mentioned in the main text of the paper, we leave out the keyword "reasoning traces", because after manual inspection, the model overuses that keyword for documents that do not actually have step-by-step reasoning. The results for the 7B slopes questions are shown below.
For the slopes questions, the most common keyword besides "other" is similar arithmetic on similar numbers, given to about 75% of the query-document pairs. Here, we show an example that gets the keyword "Math that calculates the slope of an equation".
We see that the document indeed calculates the slope between two numbers. The document starts in the middle of this calculation, but similar reasoning steps as required in the query are part of it. The model gave the following justification for choosing these keywords:
For the linear equation queries, the keyword "math that contains linear equations but they are not solved" can also occur multiple times per query-document pairs, because the model is asked to specify what type of linear equation is used (ax + b = c or another form), and we grouped them together because it was not clear when the model decided to use the one or the other. Similarly for "similar algebraic operations on similar numbers", more than 10000 occurrences can happen because we grouped "similar algebraic operations on similar numbers" and "similar algebraic operations (on other numbers, e.g. much larger/smaller)" together, for the same reason.
Below, we show an example of a query-document pair where "math that contains linear equations but they are not solved" occurs twice. The username and date occurring in this document (from the Refinedweb dataset) are redacted for privacy purposes.
It is not fully clear why the model chose to include it twice, as only linear equations of the type ax + b < or > c very clearly occur in the document. The justification the model gives also does not really clear it up.
Finally, we look at the slopes questions for the 35B model. Again, similar arithmetic on similar numbers occurs for almost all query-document pairs, and code that contains arithmetic occurs often as well.
We show an example of a query-document pair to which Command R+ ascribes both the keywords "math that calculates the slope of an equation" and "math that calculates the slope between two numbers".
We see that indeed this document does both. The model gives the following justification.
For the same query, we give another example where the model assigns the keyword "code that calculates the slope between two numbers (Java)"
The document is messy, but it indeed calculates the slope between two numbers in Java. The model gives the following justification:
We see that the model also chooses "other", for the part of the document that does trigonometry.
All in all, we conclude the documents are mostly related to the queries in procedure. They often contain similar types of arithmetic, and also often contain procedures to calculate a solution. We share some of the 20 unique documents we found manually that calculate the slope in maths or code in the supplemental material and the demo.
7B vs 35B
Although we find less unique slope procedures for the 35B (8 versus 18), they occur more often in the top 100 documents for the slope queries (51 times for thet 35B versus 38 times for the 7B). This connects to the finding of higher correlation for the slopes queries by the 35B than the 7B. Further, 6 of the documents with slope procedures occur in the top 100 documents for both models.
What are the most influential pretraining data sources?
We look at the type of source datasets that represent the most influential documents. Specifically, we count the source datasets of the top and bottom \(k\) documents with \(k \in \{50, 500, 5000, 50000, 500000\}\), and compare the count to the pretraining distribution. The results for the top portions of the rankings can be seen below.
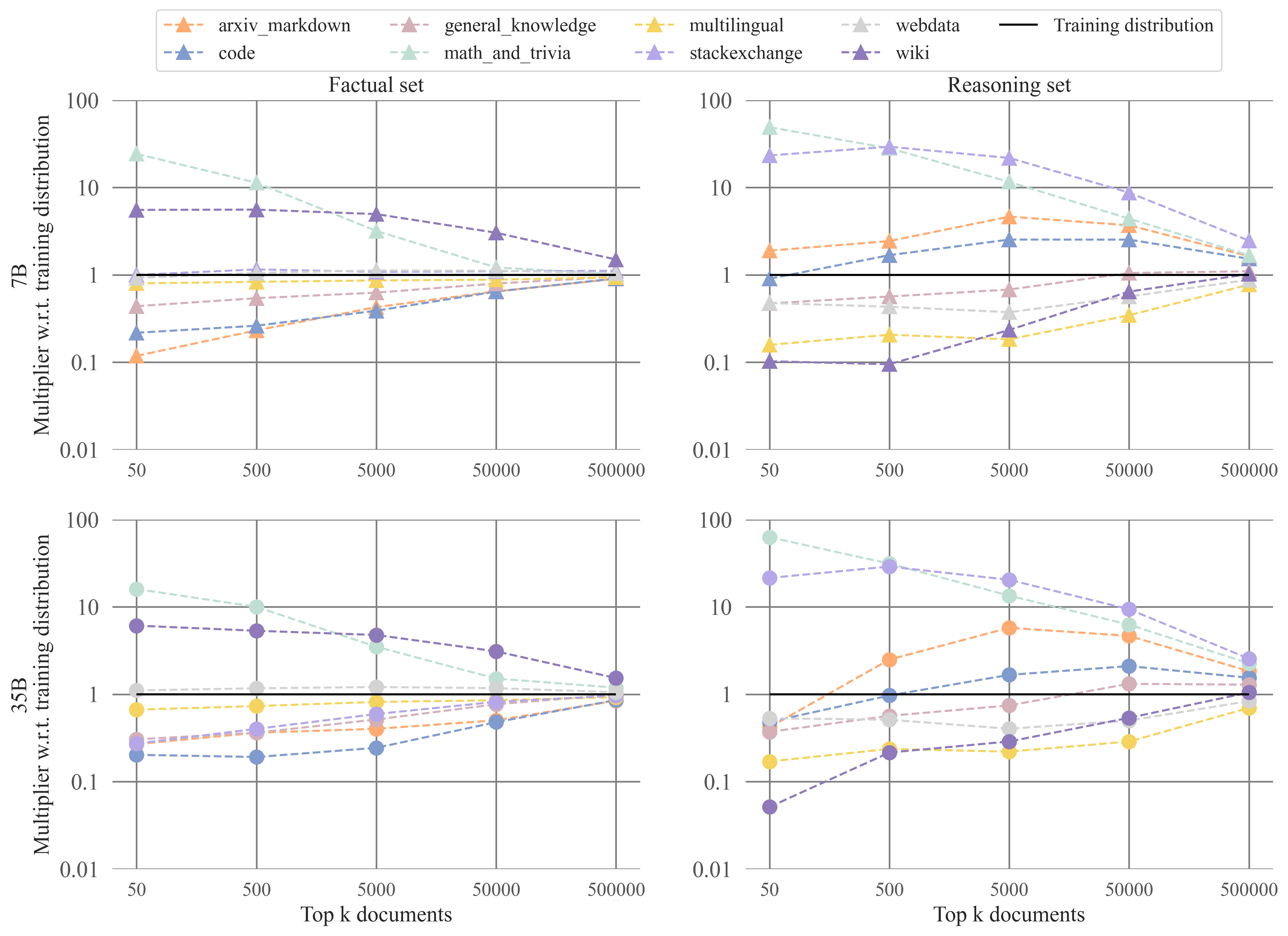
And the results for the bottom portions of the rankings:
We observe that code data is highly influential for reasoning. StackExchange as a source has more than ten times more influential data in the top and bottom portions of the rankings than expected if the influential data was randomly sampled from the pretraining distribution. Other code sources and ArXiv & Markdown are twice or more as influential as expected when drawing randomly from the pretraining distribution for middle parts of the ranking (\(k=50\) up to \(k=50000\), both for the top and bottom). For factual questions by contrast, code, stackexchange, and ArXiv & Markdown are underrepresented w.r.t. the training distribution in the top and bottom portions of the rankings. Instead, Wiki and Math & Trivia are overrepresented sources for the factual questions.
In the deep-dive below, we show the same plots for the factual and reasoning control queries, to demonstrate that the source distributions look somewhat similar for these, even though they do not require factual retrieval or reasoning. The main difference between the results for the control queries and the main queries is that: (1) Wiki is much less / not overrepresented for the factual control queries and (2) arXiv & Markdown is less / not overrepresented for the reasoning queries. The former makes sense given that Wiki likely contains information about the main factual queries, but not about the made-up fictional factual control queries. Perhaps finding (2) then also indicates something about arXiv & Markdown as a source for reasoning.
Deep-dive into finding 5 (click to view)
In this deep-dive, we look into the overrepresented and underrepresented sources for the control queries.
Recall that we have factual and reasoning control queries (10 each, different ones for both models) that do not require any factual retrieval or reasoning to be resolved. Below, we show the distribution of source datasets w.r.t. the pretraining distribution for the factual and reasoning control sets. Before we do, we show two side-by-side comparisons of a factual query and a matched factual control query that is meant to be superficially similar but not require retrieval. Similarly, the reasoning control query is meant to be similar to the reasoning prompt, but does not require any step-by-step mathematical reasoning.
We also calculated the overrepresented sources for the top and bottom portions of the rankings for the control queries. We show the results for the top portion of the rankings below:
And the results for the same set of queries for the bottom portions of the rankings:
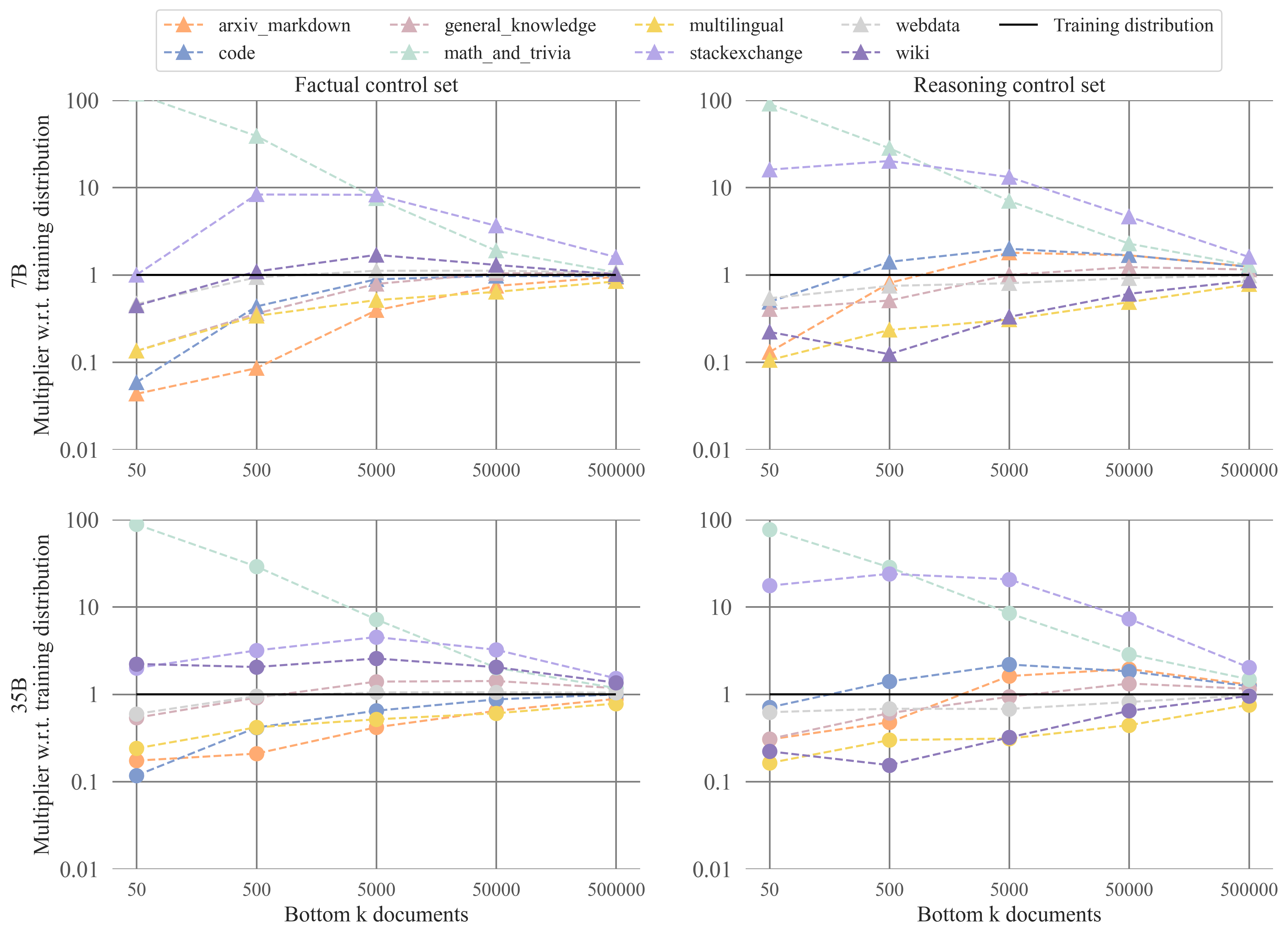What we observe is that actually the patterns are very similar to the overrepresented and underrepresented sources for the reasoning and factual queries: Math & trivia are overrepresented for the top and bottom portions of the factual control rankings, and StackExchange is additionally overrepresented for the reasoning control queries. However, the deviations can tell us something about sources that are truly influential for factual retrieval and reasoning beyond mere superficial similarities. What we see is that Wiki is much less overrepresented for the factual control queries. Further, for the reasoning control queries, arXiv & Markdown is much less overrepresented. Perhaps these two sources are truly influential for factual retrieval and reasoning.
An interesting direction for future work would be to elucidate what kind of code is positively influential, and what kind of code is negatively influential for reasoning.
Conclusion
Our findings indicate LLMs can actually learn a generalisable approach to reasoning from pretraining data, and can learn from procedural knowledge in the data. Further, we find no evidence for models relying on answers to simple mathematical reasoning steps in the pretraining data. This means the approximate retrieval hypothesis is not always true, which has important implications for the design of future AI. Namely, we likely do not need to focus on covering every case in pretraining data but can rather focus on data applying and demonstrating procedures for diverse reasoning tasks.
How can we square these findings with the well-documented brittleness and prompt-dependency of LLM reasoning, as well as the issues with evaluation data contamination? I would say that these results can exist next to each other. We showed that models seem in principle able to learn a generalisable strategy for reasoning that does not rely on retrieval but instead on procedural knowledge. That does not mean that there exist no reasoning types for which the model uses a different, more retrieval-like strategy. For example, if the answers to particular reasoning questions occur too often in the pretraining data I expect the model to memorise them, which is another reason to focus on diverse procedural data instead. Probably contamination is good for performance on the same benchmarks, and bad for general robustness of reasoning. Additionally, LLMs without access to tools clearly don’t do formal reasoning in a sense that that they apply programs to variables, and their reasoning is still dependent on pretraining statistics, even if they do not need to see answers to questions.
Importantly, we do not find evidence for models generalising from pretraining data about one particular type of reasoning to another similar one (e.g. from solving linear equations to calculating slopes of a line between two points). I am very excited about the future direction this work informs. How far can procedural generalisation from next-token prediction go? Does a type of pretraining data exist that is influential for multiple different types of reasoning, perhaps for larger models (e.g. code)?
For now, I will end by concluding our findings highlight the surprising capabilities that can emerge by scaling the next-token prediction objective.